-
JUNOLG 로봇 진행중...1일지 2023. 2. 28. 13:47
Intermediate_Coder/그래프탐색-BFS/로봇
문제
많은 공장에서 로봇이 이용되고 있다.
우리 공장의 로봇은 바라보는 방향으로 궤도를 따라 움직이며 움직이는 방향은 동, 서, 남, 북 가운데 하나이다.
로봇의 이동을 제어하는 명령어는 다음과 같이 두 가지이다.
*명령 1. Go k
- k 는 1 2 또는 3일 수 있다. 현재 향하고 있는 방향으로 k 칸만큼 움직인다.*명령 2. Turn dir
- dir 은 left 또는 right 이며 각각 왼쪽 또는 오른쪽으로 90° 회전한다.공장 내 궤도가 설치되어 있는 상태가 아래와 같이 0과 1로 이루어진 직사각형 모양으로 로봇에게 입력된다.
0은 궤도가 깔려 있어 로봇이 갈 수 있는 지점이고 1은 궤도가 없어 로봇이 갈 수 없는 지점이다.
로봇이 (4, 2) 지점에서 남쪽을 향하고 있을 때
이 로봇을 (2, 4) 지점에서 동쪽으로 향하도록 이동시키는 것은 아래와 같이 9번의 명령으로 가능하다.
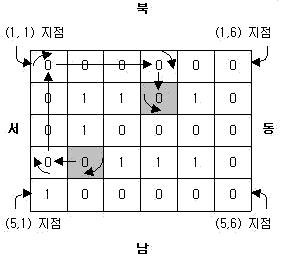
JUNGOL 그래프탐색-BFS 로봇 로봇의 현재 위치와 바라보는 방향이 주어졌을 때 로봇을 원하는 위치로 이동시키고 원하는 방향으로 바라보도록 하는데
최소 몇 번의 명령이 필요한지 구하는 프로그램을 작성하시오.
입력 형식
첫째 줄에 공장 내 궤도 설치 상태를 나타내는 직사각형의 세로 길이 M과 가로 길이 N이 빈칸을 사이에 두고 주어진다.
이 때 M과 N은 둘 다 100이하의 자연수이다.
이어 M줄에 걸쳐 한 줄에 N개씩 각 지점의 궤도 설치 상태를 나타내는 숫자 0 또는 1이 빈칸을 사이에 두고 주어진다.
다음 줄에는 로봇의 출발 지점의 위치 (행과 열의 번호)와 바라보는 방향이 빈칸을 사이에 두고 주어진다.
마지막 줄에는 로봇의 도착 지점의 위치 (행과 열의 번호)와 바라보는 방향이 빈칸을 사이에 두고 주어진다.
방향은 동쪽이 1, 서쪽이 2, 남쪽이 3, 북쪽이 4로 주어진다. 출발지점에서 도착지점까지는 항상 이동이 가능하다.
출력 형식
첫째 줄에 로봇을 도착 지점에 원하는 방향으로 이동시키는데 필요한 최소 명령 횟수를 출력한다.
입력 예
5 6
0 0 0 0 0 0
0 1 1 0 1 0
0 1 0 0 0 0
0 0 1 1 1 0
1 0 0 0 0 0
4 2 3
2 4 1출력 예
9
Robot.h
#pragma once #include <iostream> #include <queue> #include "../../Base.h" using std::queue; class Robot : public Base { protected: struct Direction { int x, y; }; struct Position { int x, y; int cost; int direction; int sameCount; bool IsSameDirection(int dir) { return direction == dir; } int GetMoveCost(int dir) { int cost = GetTurnCost(dir); // 다른 방향으로 최초 이동 시 비용이 들어간다. if (IsSameDirection(dir) == false) { cost += 1; } return cost; } int GetTurnCost(int dir) { int cost = 1; // 같은 방향은 코스트가 들지 않는다. if (IsSameDirection(dir)) { cost = 0; } // 반대 방향은 두 번 돌아야 하므로 비용이 2가 된다. else if (direction == 0 && dir == 1 || direction == 1 && dir == 0 || direction == 2 && dir == 3 || direction == 3 && dir == 2) { cost = 2; } return cost; } int GetSameCount(int dir) { if (IsSameDirection(dir)) { return sameCount + 1; } return 0; } void CheckSameCount() { if (sameCount < 3) { return; } cost += 1; sameCount = 1; } }; public: virtual void Code() override; private: int GetLeastCostToGo(); bool IsArrive(const Position& p) const; bool CanMoveTo(const Position& p) const; bool IsInMap(const Position& p) const; private: const Direction directionToMove[4]{ {1, 0}, {-1, 0}, {0, 1}, {0, -1} }; int m, n; bool map[101][101]{}; queue<Position> q; Position start, end; };Robot.cpp
void Robot::Code() { std::cin >> m >> n; int inVal; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { std::cin >> inVal; map[i][j] = (inVal == 0); } } std::cin >> start.y >> start.x >> start.direction; std::cin >> end.y >> end.x >> end.direction; // 0 부터 시작할 수 있도록 보정 start.y--; start.x--; start.direction--; end.y--; end.x--; end.direction--; start.cost = 0; start.sameCount = 1; map[start.y][start.x] = false; std::cout << GetLeastCostToGo(); } /// <summary> /// 이동하는데 필요한 최소 명령 횟수를 반환한다. /// </summary> /// <returns>최소 명령 횟수</returns> int Robot::GetLeastCostToGo() { int leastCost = 999'999'999; q.push(start); while (q.empty() == false) { Position p = q.front(); q.pop(); if (IsArrive(p)) { if (leastCost > p.cost) { // 방향을 맞추는 비용을 더한다. leastCost = p.cost + p.GetTurnCost(end.direction); } continue; } for (int i = 0; i < 4; i++) { Position newP{ p.x + directionToMove[i].x, p.y + directionToMove[i].y, p.cost + p.GetMoveCost(i), i, p.GetSameCount(i) }; newP.CheckSameCount(); if (CanMoveTo(newP)) { q.push(newP); map[newP.y][newP.x] = false; } } } return leastCost; } /// <summary> /// 도착 했는지 여부를 반환한다. /// </summary> /// <param name="p">확인할 지점</param> /// <returns>도착 여부</returns> bool Robot::IsArrive(const Position& p) const { return p.x == end.x && p.y == end.y; } /// <summary> /// 새로운 위치로 이동할 수 있는지 여부를 반환한다. /// </summary> /// <param name="p">확인할 지점</param> /// <returns>이동 가능한지 여부</returns> bool Robot::CanMoveTo(const Position& p) const { if (IsInMap(p) == false) { return false; } return map[p.y][p.x]; } /// <summary> /// 새로운 위치가 맵 안에 들어가는지 여부를 반환한다. /// </summary> /// <param name="p">확인할 지점</param> /// <returns>맵 안에 있는지 여부</returns> bool Robot::IsInMap(const Position& p) const { if (p.x < 0) return false; if (p.x >= n) return false; if (p.y < 0) return false; if (p.y >= m) return false; return true; }
실행 결과 Accepted(40)
원인 아마 같은 방향으로 이동하는 카운트 세는 방식에 문제가 있는 것으로 보인다.
처리 방법 회전과 이동을 분리해서 처리하면 확인이 가능할 것 같다.
NadanKim/CodingTest_JUNGOL: JUNGOL 코딩 테스트를 위한 저장소 (github.com)
NadanKim/CodingTest_JUNGOL
JUNGOL 코딩 테스트를 위한 저장소. Contribute to NadanKim/CodingTest_JUNGOL development by creating an account on GitHub.
github.com