JUNGOL/Intermediate_Coder/그래프탐색-DFS/3230 : 두 로봇

Intermediate_Coder/그래프탐색-DFS/두 로봇

---

문제                                            

2018년 강원도에서 새로운 동굴이 발견되었다. 

이 동굴에는 총 N개의 넓은 방이 존재하며 좁은 통로로 서로 연결되어 있는 것으로 밝혀졌다. 
N​개의 방은 1번부터 N​번까지의 번호를 붙여 1번방, 2번 방, …, N​번 방으로 부른다. 
통로는 정확히 N​-1개가 발견되었는데, 각각 서로 다른 두 방 사이를 연결시켜주며 중간에 다른 통로와 이어지는 경우는 없다고 한다. 
또한 이 통로들을 이용하여 임의의 두 방 사이를 이동하는것이 가능하며, 
임의의 두 방 사이를 이동할 때 같은 통로를 두 번 이상 지나지 않는 경로는 유일한 것으로 밝혀졌다.

새로 발견된 동굴을 조사하기 위해 동굴 탐사 로봇 두 대를 이용하기로 하였다.
두 로봇은 어떤 시점이 되면 각자가 획득한 정보를 공유하기 위해 통신을 해야 한다.
두 로봇이 서로 통신을 하기 위해서는 동굴 내의 같은 통로 위에 위치해야만 한다.
참고로 임의의 통로의 양 끝에 위치한 두 방들도 그 통로 위에 위치해 있다고 간주한다.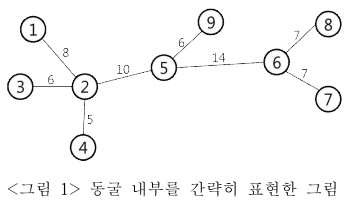

 

JUNGOL 그래프탐색-DFS 두 로봇

<그림 1>은 방이 9개인 동굴 내부를간략하게 나타낸 예이다. 
<그림 1>에서 방은 원으로 표현되어 있으며 원 안의 수는 방 번호이다. 
8개의 통로는 두 원 사이의 선분으로 표시되어 있으며 그 위의 정수 값이 통로의 길이이다. 
예를 들어, 5번 방과 9번 방 사이에 길이가 6인 통로가 있음을 알 수 있다.
만약 두 로봇이 1번 방과 9번 방에 위치해 있다면, 
각각 2번 방과 5번 방으로 이동한 후 통신할 수 있으며 이때 이동한 거리의 합은 14로 최소이다.

동굴 내의 통로에 대한 정보와 두 로봇의 현재 위치가 입력으로 주어질 때, 
서로 통신하기 위해 이동해야 하는 거리의 합의 최솟값을 계산하는 프로그램을 작성하시오. 

동굴의 각 통로는 양 끝에 위치한 두 방의 번호와 그 길이로 주어진다. 
두 로봇의 위치는 방 번호로 주어진다.

소스파일의 이름은 robot.c 또는 robot.cpp를 권장하지만, 서버에 제출하는 데는 다른 이름도 상관없다.

 

입력 형식                                     

표준 입력으로 동굴의 방의 개수 N과 두 로봇이 위치한 방의 번호가 세 개의 양의 정수로 공백으로 분리되어 첫 줄에 주어진다.
이후 동굴의 통로 N-1개가 한 줄에 하나씩 주어진다. 
각 통로는 세 개의 양의 정수로 공백으로 분리되어 한 줄에 주어지며, 
앞 두 정수는 통로의 양 끝에 위치한 방의 번호를, 
세 번째 정수는 그 통로의 길이를 의미한다.

 

출력 형식                                     

표준 출력으로 두 로봇이 서로 통신하기 위해 현재 위치에서 이동해야 하는 거리의 합의 최솟값을 정수로 출력한다.

 

[부분문제의 제약 조건] 

모든 부분문제에서 1 ≤ N ≤ 100,000이며, 통로의 길이는 1,000을 넘지 않는다. 

* 부분문제 1: 전체 점수 100점 중 17점에 해당하며, 

  입력에서 두 번째 줄에 주어지는 방번호는 1과 2,

  세 번째 줄에 주어지는 방 번호는 2와 3, …,

  i 번째 줄에 주어지는 방 번호는 i-1과 i, …, 

  N번째 줄에 주어지는방 번호는 N-1과 N이다(아래 입력과 출력의 예에서 입력(1)을 참고). 

* 부분문제 2: 전체 점수 100점 중 19점에 해당하며 동굴 내의 통로의 길이가 모두 1이다. 

* 부분문제 3: 전체 점수 100점 중 23점에 해당하며 N ≤ 5,000 이다. 

* 부분문제 4: 전체 점수 100점 중 41점에 해당하며 공통조건 이외에 제약조건이 없다.

 

입력 예                                        

5 1 5            | 9 1 9
1 2 1            | 1 2 8
2 3 2            | 2 3 6
3 4 3            | 2 4 5
4 5 4            | 2 5 10

                   | 9 5 6

                   | 6 5 14

                   | 6 7 7

                   | 8 6 7

 

출력 예                                        

6                 | 14

---

Robot.h

#include <iostream>
#include <vector>

using std::vector;

class Robot : public Base
{
private:
	struct WayInfo
	{
		WayInfo(int to, int cost) : to(to), cost(cost) {}

		int to;
		int cost;
	};

	int GetMinimumDistance(const vector<vector<WayInfo>>& rooms, bool isChecked[], int n, 
		int r1, int r2, int total = 0, int maximum = 0);
};

 

Robot.cpp

void Robot::Code()
{
	int n, r1, r2;
	std::cin >> n >> r1 >> r2;

	vector<vector<WayInfo>> rooms(n + 1, vector<WayInfo>());

	int from, to, cost;
	for (int i = 1; i < n; i++)
	{
		std::cin >> from >> to >> cost;

		rooms[from].push_back(WayInfo(to, cost));
		rooms[to].push_back(WayInfo(from, cost));
	}

	bool* isChecked = new bool[n] {};
	std::cout << GetMinimumDistance(rooms, isChecked, n, r1, r2);
	delete[] isChecked;
}

/// <summary>
/// 두 로봇이 통신 가능한 최소 이동 거리를 구하여 반환한다.
/// </summary>
/// <param name="rooms">방 정보</param>
/// <param name="isChecked">방문 여부</param>
/// <param name="n">방 개수</param>
/// <param name="r1">로봇1 위치</param>
/// <param name="r2">로봇2 위치</param>
/// <param name="total">총 이동 거리</param>
/// <param name="maximum">경로간 단일 최대 이동 거리</param>
/// <returns>최소 이동 거리</returns>
int Robot::GetMinimumDistance(const vector<vector<WayInfo>>& rooms, bool isChecked[], int n,
	int r1, int r2, int total, int maximum)
{
	if (r1 == r2)
	{
		return total - maximum;
	}

	int result{ 0 };
	if (!isChecked[r1])
	{
		isChecked[r1] = true;

		for (const WayInfo& room : rooms[r1])
		{
			result = GetMinimumDistance(rooms, isChecked, n, room.to, r2, total + room.cost, std::max(maximum, room.cost));
			if (result > 0)
			{
				break;
			}
		}
	}

	return result;
}

 

---

실행 결과 Success(100)

---

 

코드 해설

두 로봇이 통신 가능한 최소 거리는 결국 한 로봇이 다른 로봇을 찾을 수 있는 경로에서 비용이 가장 큰 값을 제외한 것이 최소 비용이 될 것이다.

 

적절하게 길을 찾기 위해 각 방에서 이동 가능한 경로를 모두 저장한다.

	for (int i = 1; i < n; i++)
	{
		std::cin >> from >> to >> cost;

		rooms[from].push_back(WayInfo(to, cost));
		rooms[to].push_back(WayInfo(from, cost));
	}

 

이후 재귀적으로 길을 찾음과 동시에 비용을 누적한다.

result = GetMinimumDistance(rooms, isChecked, n, room.to, r2, total + room.cost, std::max(maximum, room.cost));

 

최종적으로 두 로봇이 같은 위치에 도달했을 때 누적한 비용에서 가장 큰 비용을 빼준다.

	if (r1 == r2)
	{
		return total - maximum;
	}

 

NadanKim/CodingTest_JUNGOL: JUNGOL 코딩 테스트를 위한 저장소 (github.com)

NadanKim/CodingTest_JUNGOL

 

문제출처

Intermediate_Coder/그래프탐색-DFS/두 로봇-JUNGOL