KD 트리 알고리즘

  KD 트리 

이진 검색 트리를 다차원 검색 트리로 확장한 트리 자료구조이다.

 

KD 트리는 같은 레벨의 노드는 동등한 위치의 필드를 사용하여 분기를 진행하며 k 개의 필드를 가지는 KD 트리에서 레벨 k에 도달한 경우 다시 0 번째 필드를 사용하여 분기를 진행한다.

 

※ 다차원 검색 트리는 노드의 키가 하나의 필드가 아닌 여러 개의 필드로 이루어진 검색 트리를 말한다.

 

KD 트리에서의 검색

기본적으로 이진 검색 트리와 동일한 방식으로 탐색을 진행하나 KD 트리는 각 레벨 별로 다른 필드를 사용하여 검색을 진행하는 점이 다르다.

 

레벨 0 에서는 첫 번째 필드를 사용하여 분기하고 레벨 1에서는 두 번째 필드를 사용하여 분기를 진행한다.

이렇게 진행하다 레벨 k 에서는 다시 첫 번째 필드를 사용하는 방식으로 검색을 진행한다.

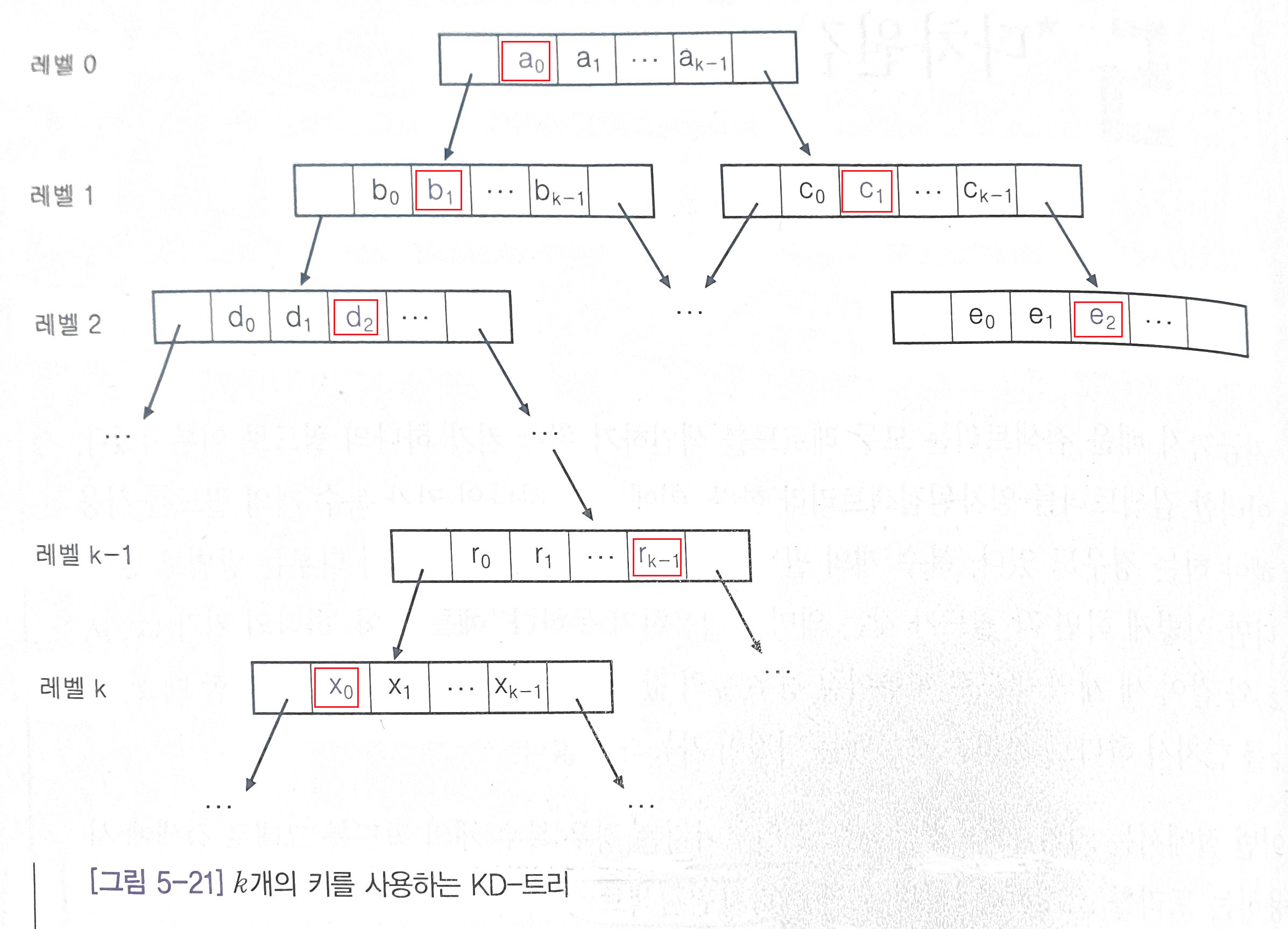
쉽게 배우는 알고리즘 KD 트리 그림 5-21

 

 

KD 트리에서의 삽입

이진 검색 트리와 동일한 방식으로 삽입이 진행되나 말단 노드를 검색하기 위한 과정에서 레벨 별로 다른 필드를 사용한다는 점이 다르다.

 

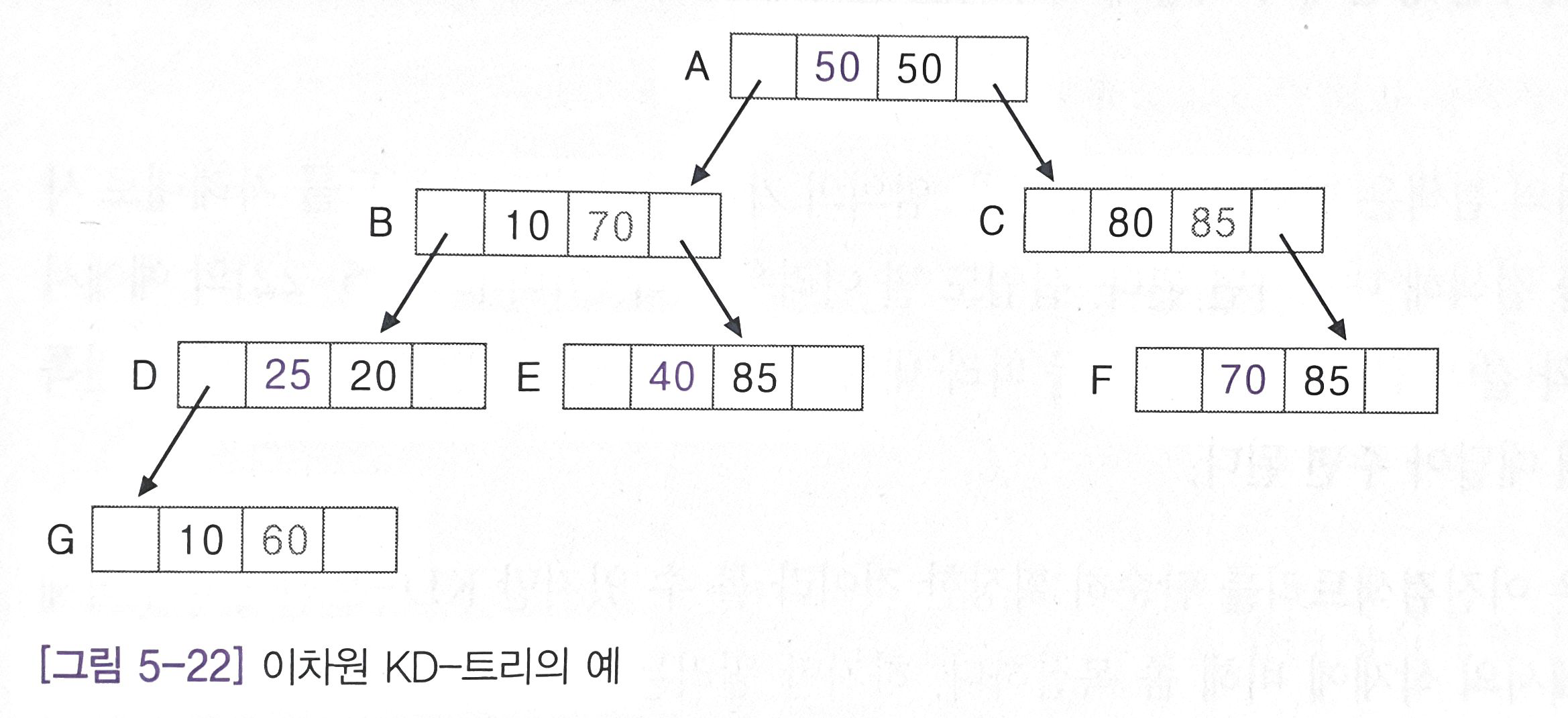
KD 노드에 (50, 50), (10, 70), (80, 85), (25, 20), (40, 85), (70, 85), (10, 60) 를 순서대로 삽입하는 경우 다음과 같은 순서로 삽입이 진행되게 된다.

1. 트리가 비어있으므로 (50, 50)을 루트로 삽입하고 종료한다.
2. 루트의 첫 번째 필드와 비교하여 10이 50보다 작으므로 왼쪽 자식으로 이동한다.
   1. 왼쪽 자식이 비어있으므로 (10, 70)을 삽입하고 종료한다.
3. 루트의 첫 번째 필드와 비교하여 80이 50보다 크므로 오른쪽 자식으로 이동한다.
   1. 오른쪽 자식이 비어있으므로 (80, 85)를 삽입하고 종료한다.
4. 루트의 첫 번째 필드와 비교하여 25가 50보다 작으므로 왼쪽 자식으로 이동한다.
   
   1. 왼쪽 자식의 두 번째 필드와 비교하여 20이 70보다 작으므로 왼쪽 자식으로 이동한다.
   2. 왼쪽 자식이 비어있으므로 (25, 20)을 삽입하고 종료한다.
5. 루트의 첫 번째 필드와 비교하여 40이 50보다 작으므로 왼쪽 자식으로 이동한다.
   1. 왼쪽 자식의 두 번째 필드와 비교하여 85가 70보다 크므로 오른쪽 자식으로 이동한다.
   2. 오른쪽 자식이 비어있으므로 (40, 85)를 삽입하고 종료한다.
6. 루트의 첫 번째 필드와 비교하여 70이 50보다 크므로 오른쪽 자식으로 이동한다.
   1. 오른쪽 자식의 두 번째 필드와 비교하여 85가 85와 같으므로 오른쪽 자식으로 이동한다.
   2. 오른쪽 자식이 비었으므로 (70, 85)를 삽입하고 종료한다.
7. 루트의 첫 번째 필드와 비교하여 10이 50보다 작으므로 왼쪽 자식으로 이동한다.
   1. 왼쪽 자식의 두 번째 필드와 비교하여 60이 70보다 작으므로 왼쪽 자식으로 이동한다.
   2. 왼쪽 자식의 첫 번째 필드와 비교하여 10이 25보다 작으므로 왼쪽 자식으로 이동한다.
   3. 왼쪽 자식이 비었으므로 (10, 60)을 삽입하고 종료한다.

 

쉽게 배우는 알고리즘 KD 트리 그림 5-22

 

KD 트리에서의 삭제

이진 검색 트리와 동일한 방식으로 삭제를 진행되나 자식이 하나라도 단순히 자식 노드를 기존 노드에 대체하면 레벨별로 사용한 필드가 다르기 때문에 KD 트리의 속성이 깨지게 된다.

 

따라서 KD 트리에서는 말단 노드를 제거할 때 외에는 자식 노드가 두 개 있을 때의 처리를 진행한다.

 

- 자식이 둘 일 때의 처리

삭제할 노드의 오른쪽 서브 트리에서 삭제할 노드의 레벨에서 사용한 필드가 가장 작은 노드를 찾아 값을 교환하고 찾은 노드를 삭제한다.

 

※ 찾은 노드가 자식을 가진 경우 이상의 처리를 반복한다.

 

- 삭제 처리 예제

루트 노드를 삭제할 때의 처리 과정을 보여준다.

 

쉽게 배우는 알고리즘 KD 트리 그림 5-24

 

- 삭제 시 적절한 노드를 찾는 과정

삭제 시에는 레벨에 따라 노드를 확인해야 하므로 트리에 깊이에 따라 시간이 늘어나게 된다.

따라서 제외 가능한 노드를 빠르게 제외하여 검사 수를 줄여야 한다.

 

위 예제에서 A를 제거하면서 오른쪽 서브 트리에서 첫 번째 필드가 가장 작은 값을 찾을 때 C의 왼쪽 자식인 E의 오른쪽 서브 트리는 E 보다 클 것이므로 볼 필요가 없으니 제외한다.

 

마찬가지로 C의 오른쪽 자식인 F의 오른쪽 자식도 볼 필요가 없으므로 제외하면 4번의 검사만으로 첫 번째 필드가 가장 작은 노드를 찾을 수 있다.

 

쉽게 배우는 알고리즘 KD 트리 그림 5-25

 

NadanKim/Algorithm: 알고리즘 학습 및 예제 코드 작성을 위한 저장소 (github.com)

GitHub - NadanKim/Algorithm: 알고리즘 학습 및 예제 코드 작성을 위한 저장소

 

참고문헌

한빛아카데미.문병로.(2016.07.24).쉽게 배우는 알고리즘