-
트리(Tree)와 이진 탐색 트리(Binary Search Tree)프로그래밍 기초/자료구조 2021. 3. 29. 19:33
트리
각각의 자료가 노드를 이루고 각 노드가 부모-자식 관계를 형성하는 자료구조를 말한다.
트리의 구성 요소
트리는 하나의 루트와 여러 개의 자식 노드로 구성된다.
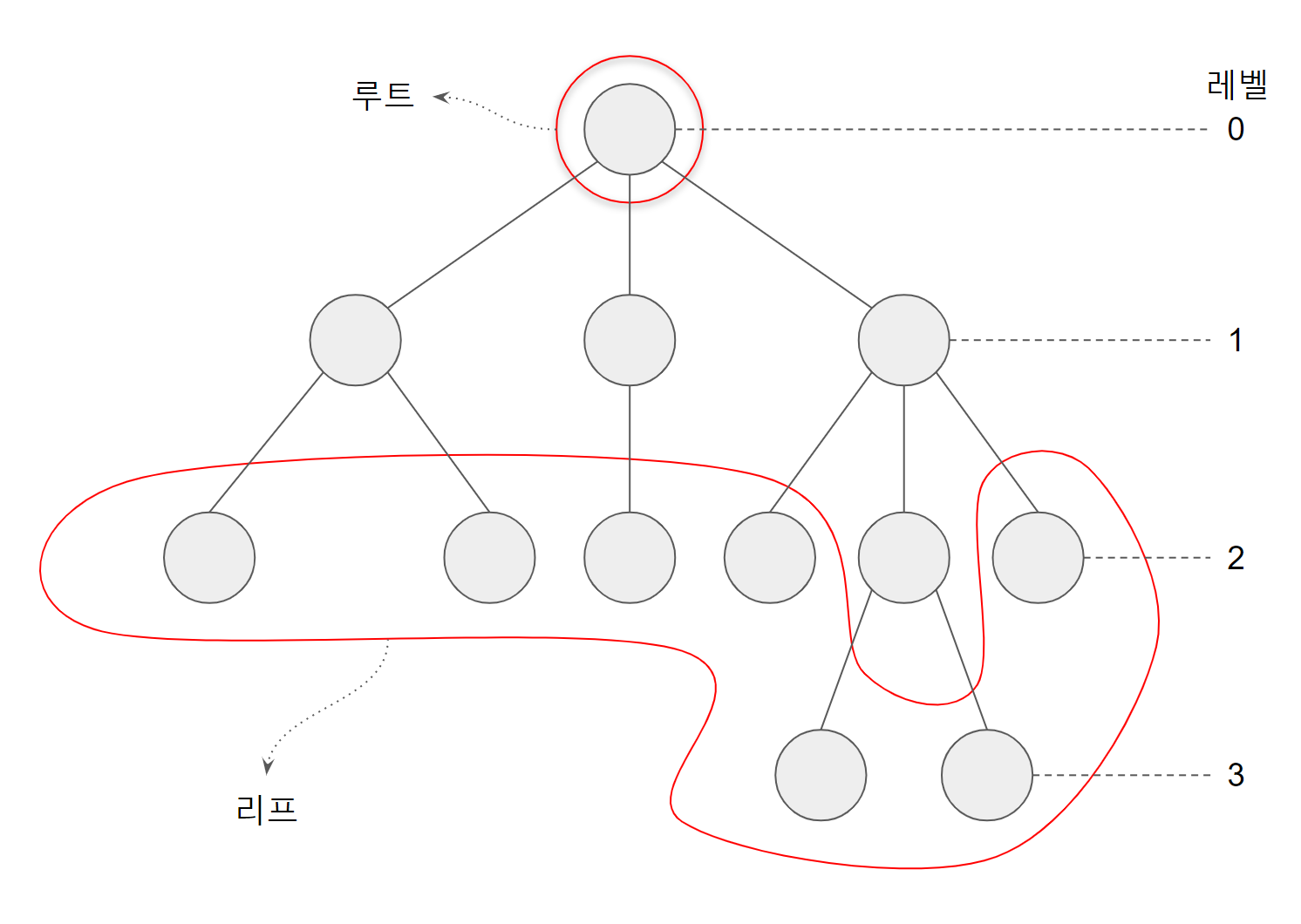
- 노드 트리를 이루는 각각의 요소
- 루트 트리의 최상단 요소
- 리프 트리의 최말단 요소
- 차수 각 노드가 가진 자식의 수
- 트리의 차수 해당 트리에 존재하는 각 노드의 차수 중 가장 큰 값
- 높이 트리의 노드의 레벨 중 가장 큰 값
이진트리
리프 노드를 제외한 노드의 자식이 1개 혹은 2개로 이루어진 트리로 각 서브 트리는 다음과 같은 구조로 이루어진다.

※ 각 자식 노드를 왼쪽 자식 노드와 오른쪽 자식 노드로 구분하며 각각의 자식 노드가 자식 노드를 가진 경우 자식 노드를 루트로 하는 노드 집단을 서브 트리라고 한다.
이진 트리의 특징
- n개의 노드를 진 경우 n-1 개의 간선을 가진다.
- 높이가 h인 이진트리가 가질 수 있는 노드의 최소 개수는 h-1 개이며 최대 개수는 2^(h+1)-1 개가 된다.
이진 트리의 분류
- 포화 이진 트리 모든 리프 노드의 높이가 h이고 리프 느도를 제외한 모든 노드가 두개의 자식을 가지는 경우
- 완전 이진 트리 포화 이진 트리에서 마지막 리프 노드가 빈 경우
- 편향 이진 트리 모든 노드가 왼쪽 자식만을 가지거나 오른쪽 자식만을 가지는 경우

이진 트리의 순회
이진 트리에 존재하는 모든 노드를 한 번씩 방문하여 데이터를 처리하는 과정을 순회라고 하며 다음과 같이 구분한다.
- 전위 순회 데이터를 처리 후 왼쪽 노드, 오른쪽 노드 순서로 이동
- 중위 순회 왼쪽 노드로 이동한 뒤 데이터 처리 후 오른쪽 노드로 이동
- 후위 순회 왼쪽 노드로 이동한 뒤 오른쪽 노드로 이동 후 데이터 처리
이진 트리의 순회 예제

위와 같은 트리에 대해 모든 순회 방법에 따른 경로를 표시하면 다음과 같다.
- 전위 순회 A - B - D - E - C
- 중위 순회 D - B - E - A - C
- 후위 순회 D - E - B - C - A
이진 트리를 순차 자료구조로 표현하면 다음과 같이 표현할 수 있다.
인덱스 0 (root) 1 2 3 4 데이터 A B C D E root = 0 일 때
left child = (parent * 2) + 1
right child = (parent * 2) + 2
이진 탐색 트리
탐색을 위한 이진 트리로 데이터의 크기에 따라 노드의 위치를 결정한다.
이진 탐색 트리의 정의
- 모든 원소는 서로 다른 유일한 키를 갖는다.
- 왼쪽 서브 트리에 있는 원소의 키들은 그 루트의 키보다 작다.
- 오른쪽 서브 트리에 있는 원소의 키들은 그 루트의 키보다 크다.
- 왼쪽 서브 트리와 오른쪽 서브 트리도 이진 탐색 트리다.
이진 탐색 트리의 탐색 연산
값을 찾을 때에는 루트에서부터 찾으려는 값을 비교하며 진행한다.
- 노드의 값 = 찾으려는 값 탐색 성공
- 노드의 값 > 찾으려는 값 왼쪽 서브 트리로 이동하여 탐색 연산 수행
- 노드의 값 < 찾으려는 값 오른쪽 서브 트리로 이동하여 탐색 연산 수행
이진 탐색 트리의 삽입 연산
삽입하려는 값을 탐색한 뒤 트리에 값이 존재하지 않으면 값을 트리에 추가한다.

왼쪽 트리에 4를 삽입하면 다음의 과정을 거쳐 오른쪽 트리가 된다.
- 노드의 값(8) > 찾으려는 값(4) 왼쪽 서브 트리로 이동하여 탐색 연산 진행
- 노드의 값(3) < 찾으려는 값(4) 오른쪽 서브 트리로 이동하여 탐색 연산 진행
- 노드의 값(5) > 찾으려는 값(4) 왼쪽 서브 트리로 이동하여 탐색 연산 진행
- 탐색 연산 실패 해당 위치에 4를 삽입하고 연산 종료
이진 탐색 트리의 삭제 연산
삭제 연산의 경우 삭제되는 노드의 자식에 따라 연산이 달라진다.
- 자식 노드가 없는 경우 대상 노드를 제거하고 연산을 종료한다.
- 자식 노드가 하나인 경우 대상 노드를 제거하고 자식 노드와 위치를 바꾼다.
- 자식 노드가 두 개인 경우 왼쪽 자식을 선택할지 오른쪽 자식을 선택할지에 따라 연산이 달라진다.
- 왼쪽 자식에게 계승하는 경우 대상 노드 삭제 후 왼쪽 서브 트리에서 가장 큰 값을 가진 노드와 위치를 바꾼다.
- 오른쪽 자식에게 계승하는 경우 대상 노드 삭제 후 오른쪽 서브 트리에서 가장 작은 값을 가진 노드와 위치를 바꾼다.
이진 탐색 트리 구현
구현에 필요한 메서드 및 속성은 다음과 같다.
- 속성
- Count BinarySearchTree에 포함된 데이터의 개수
- Max BinarySearchTree에 추가된 데이터 중 가장 큰 값
- Min BinarySearchTree에 추가된 데이터 중 가장 작은 값
- 메서드
- Search(data) 데이터가 저장되어 있는지 여부 확인
- Insert(data) BinarySearchTree의 규칙에 맞게 데이터를 저장
- Delete(data) 일치하는 데이터를 제거하고 실행 결과를 반환
- Clear() 저장되어 있는 모든 데이터 삭제
구현 코드
BinarySearchTree.h
#pragma once #include <iostream> class BinarySearchTree { public: #pragma region 노드 struct Node { Node() {} Node(int value) { m_data = value; } int m_data{ 0 }; Node* m_left{ nullptr }; Node* m_right{ nullptr }; }; #pragma endregion #pragma region 생성자 BinarySearchTree(); ~BinarySearchTree(); #pragma endregion #pragma region 속성 const size_t Count() { return m_count; } const int Max() { if (m_root == nullptr) return 0; Node* target{ m_root }; while (target->m_left != nullptr) { target = target->m_left; } return target->m_data; } const int Min() { if (m_root == nullptr) return 0; Node* target{ m_root }; while (target->m_right != nullptr) { target = target->m_right; } return target->m_data; } #pragma endregion #pragma region 메서드 void Insert(int value); void Delete(int value); void Clear(); bool Search(int value); void PrintInfo(); private: void PrintInfo(Node* node, size_t depth = 0); #pragma endregion private: #pragma region Class Util Node* PopNode(int value); void PushNode(Node* node); #pragma endregion #pragma region 변수 size_t m_count; Node* m_root; Node* m_free; #pragma endregion };BinarySearchTree.cpp
#include "BinarySearchTree.h" #pragma region 생성자 /// <summary> /// 비어있는 BinarySearchTree를 생성한다. /// </summary> BinarySearchTree::BinarySearchTree() : m_count(0), m_root(nullptr), m_free(nullptr) { } /// <summary> /// 메모리 누수를 막기 위해 동적 생성한 노드들을 제거한다. /// </summary> BinarySearchTree::~BinarySearchTree() { Clear(); while (m_free != nullptr) { Node* curNode{ m_free }; m_free = m_free->m_right; delete curNode; } } #pragma endregion #pragma region 메서드 /// <summary> /// /// </summary> /// <param name="value">추가할 값</param> void BinarySearchTree::Insert(int value) { if (m_root == nullptr) { m_root = PopNode(value); return; } Node* target{ m_root }; while (target != nullptr) { if (target->m_data == value) { break; } if (target->m_data > value) { if (target->m_left == nullptr) { target->m_left = PopNode(value); m_count++; } target = target->m_left; } else { if (target->m_right == nullptr) { target->m_right = PopNode(value); m_count++; } target = target->m_right; } } } /// <summary> /// BinarySearchTree에서 지정된 값을 가진 노드를 제거한다. /// </summary> /// <param name="value">제거할 값</param> void BinarySearchTree::Delete(int value) { if (m_root == nullptr) { return; } Node* target{ m_root }; Node* parent{ nullptr }; while ((target != nullptr) && (target->m_data != value)) { parent = target; if (target->m_data > value) { target = target->m_left; } else { target = target->m_right; } } if (target == nullptr) { return; } if (target->m_left == nullptr && target->m_right == nullptr) { if (parent == nullptr) { m_root = nullptr; } else if (parent->m_left == target) { parent->m_left = nullptr; } else { parent->m_right = nullptr; } } else if (target->m_left != nullptr && target->m_right == nullptr || target->m_left == nullptr && target->m_right != nullptr) { Node* child{ target->m_left != nullptr ? target->m_left : target->m_right }; if (parent == nullptr) { m_root = child; } else if(parent->m_left == target) { parent->m_left = child; } else { parent->m_right = child; } } else { parent = target; Node* successor{ target->m_left }; while (successor->m_right != nullptr) { parent = successor; successor = successor->m_right; } if (parent->m_left == successor) { parent->m_left = successor->m_left; } else { parent->m_right = successor->m_left; } target->m_data = successor->m_data; target = successor; } PushNode(target); } /// <summary> /// BinarySearchTree의 모든 노드를 제거한다. /// </summary> void BinarySearchTree::Clear() { while (m_root != nullptr) { Delete(m_root->m_data); } } /// <summary> /// BinarySearchTree에 지정된 값이 존재하는지 검색한다. /// </summary> /// <param name="value">검색할 값</param> bool BinarySearchTree::Search(int value) { if (m_root == nullptr) { return false; } Node* target{ m_root }; while (target != nullptr) { if (target->m_data == value) { break; } if (target->m_data > value) { target = target->m_left; } else { target = target->m_right; } } return target != nullptr; } /// <summary> /// 테스트용 리스트 정보 출력 함수 /// </summary> void BinarySearchTree::PrintInfo() { std::cout << "----------------------\n"; PrintInfo(m_root); std::cout << "----------------------\n\n"; } /// <summary> /// 테스트용 리스트 정보 출력 함수 /// </summary> void BinarySearchTree::PrintInfo(Node* node, size_t depth) { if (node == nullptr) { return; } for (int i = 0; i < depth; i++) { std::cout << " "; } std::cout << "└ " << node->m_data << '\n'; PrintInfo(node->m_left, depth + 1); PrintInfo(node->m_right, depth + 1); } #pragma endregion #pragma region Class Util /// <summary> /// 자유 공간 리스트에서 노드를 가져오거나 새로 생성한다. /// </summary> /// <param name="value">노드 생성시 초기값</param> /// <returns>새 노드</returns> BinarySearchTree::Node* BinarySearchTree::PopNode(int value) { Node* newNode{ nullptr }; if (m_free == nullptr) { newNode = new Node(value); } else { newNode = m_free; m_free = m_free->m_right; newNode->m_data = value; newNode->m_right = nullptr; } return newNode; } /// <summary> /// 자유 공간 리스트에 제거된 노드를 저장한다. /// </summary> /// <param name="node">제거된 노드</param> void BinarySearchTree::PushNode(Node* node) { node->m_left = nullptr; node->m_right = m_free; m_free = node; } #pragma endregion테스트 코드
main.cpp
#include <iostream> #include "BinarySearchTree/BinarySearchTree.h" // 생성한 자료구조 테스트용 메인 int main() { BinarySearchTree bst; bst.Insert(5); bst.Insert(3); bst.Insert(1); bst.Insert(0); bst.Insert(4); bst.Insert(8); bst.Insert(7); bst.Insert(9); bst.PrintInfo(); bst.Delete(5); bst.PrintInfo(); std::cout << std::boolalpha << bst.Search(5) << '\n'; std::cout << std::boolalpha << bst.Search(9) << '\n'; bst.Clear(); bst.PrintInfo(); }실행 결과
---------------------- └ 5 └ 3 └ 1 └ 0 └ 4 └ 8 └ 7 └ 9 ---------------------- ---------------------- └ 4 └ 3 └ 1 └ 0 └ 8 └ 7 └ 9 ---------------------- false true ---------------------- ----------------------