-
JUNGOL 실력키우기 수학1 - 최대공약수와최소공배수 | 최대공약수, 최소공배수보관함 2020. 1. 31. 19:52
기초 다지기에서 배운 내용을 응용하여 문제를 해결해야 하는 실력 키우기입니다.
실력 키우기는 비슷한 문제 유형별로 묶어서 풀어보겠습니다.
이번 포스팅에서는 수학1의 최대공약수, 최소공배수 시리즈를 풀어보겠습니다.
1658 : 최대공약수와최소공배수
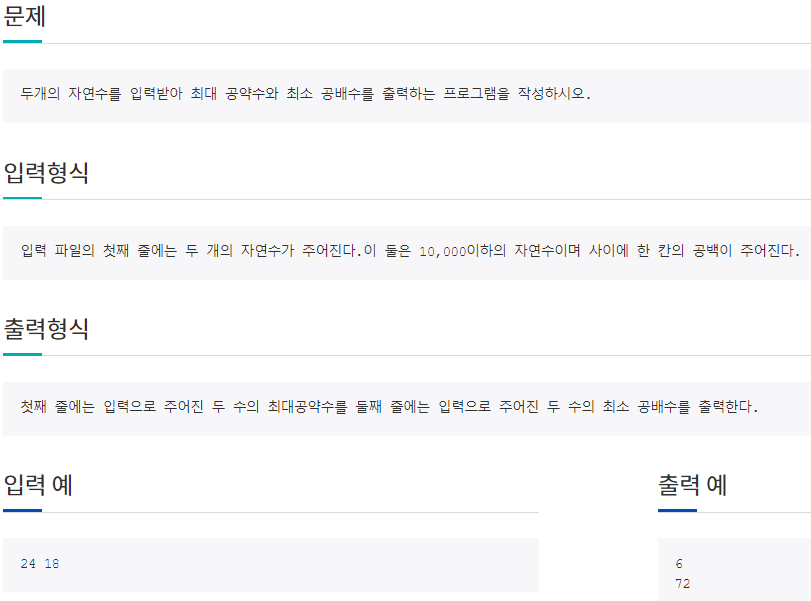
최소 공배수는 간단하게 구할 수 있는데 두 수중 한 수의 배수를 구하면서 다른 수로 나누어 떨어지는 가장 작은 수를 찾으면 됩니다.
이 문제에서 시간이 오래 걸리는 부분은 최대 공약수를 구하는 것인데 먼저 이전에 사용했던 방식으로 두 수의 약수를 모두 구하고 공통되는 가장 큰 약수를 찾는 방법이 있습니다.
#include <iostream> #include <cmath> #include <vector> using namespace std; int main(void) { int a, b; cin >> a >> b; vector<int> aFactors; int limit = static_cast<int>(sqrt(a)); for (int i = 1; i <= limit; ++i) { if (a % i == 0) { aFactors.push_back(i); if (i != a / i) { aFactors.push_back(a / i); } } } vector<int> bFactors; limit = static_cast<int>(sqrt(b)); for (int i = 1; i <= limit; ++i) { if (b % i == 0) { bFactors.push_back(i); if (i != b / i) { bFactors.push_back(b / i); } } } int maxFactor{ -1 }; for (int i = 0; i < aFactors.size(); ++i) { for (int j = 0; j < bFactors.size(); ++j) { if (aFactors[i] == bFactors[j]) { if (maxFactor < aFactors[i]) maxFactor = aFactors[i]; break; } } } int minMultiple{ a }; while (true) { if (minMultiple % b == 0) { break; } minMultiple += a; } cout << maxFactor << endl; cout << minMultiple << endl; }또, 유클리드 호제법을 사용하는 경우 더 쉽게 최대 공약수를 구할 수 있습니다.
유클리드 호제법은 A와 B의 최대 공약수는 A와 r의 최대공약수와 같다라는 내용인데, 여기에서 r은 A를 B로 나눈 나머지 입니다. 이것을 다시 쓰면 GCD(A, B) = GCD(B, A % B)입니다.
#include <iostream> using namespace std; int GetGCD(int a, int b); int main(void) { int a, b; cin >> a >> b; int maxFactor = GetGCD(a, b); int minMultiple{ a }; while (true) { if (minMultiple % b == 0) { break; } minMultiple += a; } cout << maxFactor << endl; cout << minMultiple << endl; } int GetGCD(int a, int b) { int r; while (a % b != 0) { r = a % b; a = b; b = r; } return b; }이것을 다시 재귀함수를 사용하면 다음과 같이 더욱 짧은 코드로 풀 수 있습니다.
#include <iostream> using namespace std; int GetGCD(int a, int b); int main(void) { int a, b; cin >> a >> b; int maxFactor = GetGCD(a, b); int minMultiple{ a }; while (true) { if (minMultiple % b == 0) { break; } minMultiple += a; } cout << maxFactor << endl; cout << minMultiple << endl; } int GetGCD(int a, int b) { if (b == 0) return a; return GetGCD(b, a % b); }http://www.jungol.co.kr/bbs/board.php?bo_table=pbank&wr_id=931&sca=2030
JUNGOL | 최대공약수와최소공배수 > 문제은행
입력 파일의 첫째 줄에는 두 개의 자연수가 주어진다.이 둘은 10,000이하의 자연수이며 사이에 한 칸의 공백이 주어진다. 첫째 줄에는 입력으로 주어진 두 수의 최대공약수를 둘째 줄에는 입력으로 주어진 두 수의 최소 공배수를 출력한다.
www.jungol.co.kr
1002 : 최대공약수, 최소공배수
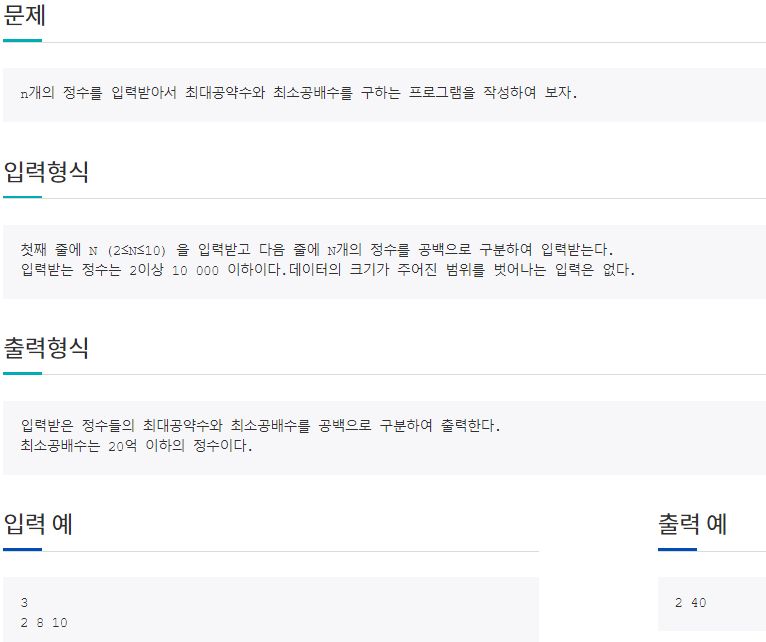
최대 공약수도 유클리드 호제법을 이용하여 구할 수 있는데 A와 B의 최대 공약수는 A / GCD(A, B) * B 로 구할 수 있다.
#include <iostream> using namespace std; int GetGCD(int a, int b); int main(void) { int n; cin >> n; int arr[10]; for (int i = 0; i < n; ++i) { cin >> arr[i]; } int gcd{ arr[0] }, lcm{ arr[0] }; for (int i = 1; i < n; ++i) { gcd = GetGCD(gcd, arr[i]); lcm = lcm / GetGCD(lcm, arr[i]) * arr[i]; } cout << gcd << ' ' << lcm << endl; } int GetGCD(int a, int b) { if (b == 0) return a; return GetGCD(b, a % b); }http://www.jungol.co.kr/bbs/board.php?bo_table=pbank&wr_id=281&sca=2030
JUNGOL | 최대공약수, 최소공배수 > 문제은행
두 개의 수 A와 B의 최대공약수를 D라 하면, 세 개의 수 A, B, C의 최대공약수는 D와 C의 최대공약수와 같다. 이런 규칙을 이용하면 두 수의 최대공약수를 구하는 함수 한 개만으로도 여러 수의 최대공약수를 구할 수 있다. 최소공배수 역시 두 수의 최소공배수를 구해 나가는 방법으로 구할 수 있다. a배열에 N개의 수가 저장되어 있다고 가정한다면 다음과 같이 구현할 수 있다. 코드 gcd = lcm = a[0];for (i=1; i < N; i+
www.jungol.co.kr