이진 검색 트리 구현 및 테스트
이진 검색 트리
이진 검색 트리의 특성은 다음과 같다.
- 각 노드는 서로 다른 키 값을 하나씩 갖는다.
- 최상위 레벨에 루트가 있으며, 각 노드는 최대 두 개의 자식 노드를 가진다.
- 노드의 왼쪽 서브 트리의 모든 노드의 값은 항상 노드의 값보다 작다.
- 노드의 오른쪽 서브 트리의 모든 노드의 값은 항상 노드의 값보다 크다.

이진 검색 트리에서의 검색
특정 키를 가진 노드를 검색하는 방법은 다음과 같다.
- 이진 검색 트리의 루트 노드에서부터 비교를 시작한다.
- 주어진 키와 노드의 키를 비교하여 주어진 키가 노드의 키가 같으면 노드를 반환한다.
- 주어진 키가 노드의 키보다 작으면 왼쪽 서브 트리로 이동하여 다시 비교한다.
- 주어진 키가 노드의 키보다 크면 오른쪽 서브 트리로 이동하여 다시 비교한다.
- 위 과정을 노드를 찾거나 말단 노드에 도달할 때까지 반복한다.

이진 검색 트리에서의 검색 알고리즘
TreeSearch(t, x)
{
if (t = NIL or key[t] = x) then return t;
if (x < key[t]) then
{
return TreeSearch(left[t], x);
}
else
{
return TreeSearch(right[t], x);
}
}
이진 검색 트리에서의 삽입
이진 검색 트리에 노드를 삽입하는 방법은 다음과 같다.
- 삽입하려는 값이 이진 검색 트리에 존재하는지 확인하기 위해 검색을 진행한다.
- 값이 이미 존재하는 경우 종료한다.
- 값이 존재하지 않아 말단 노드에 도달한 경우 해당 노드에 삽입하려는 값을 가진 노드를 추가한 뒤 종료한다.
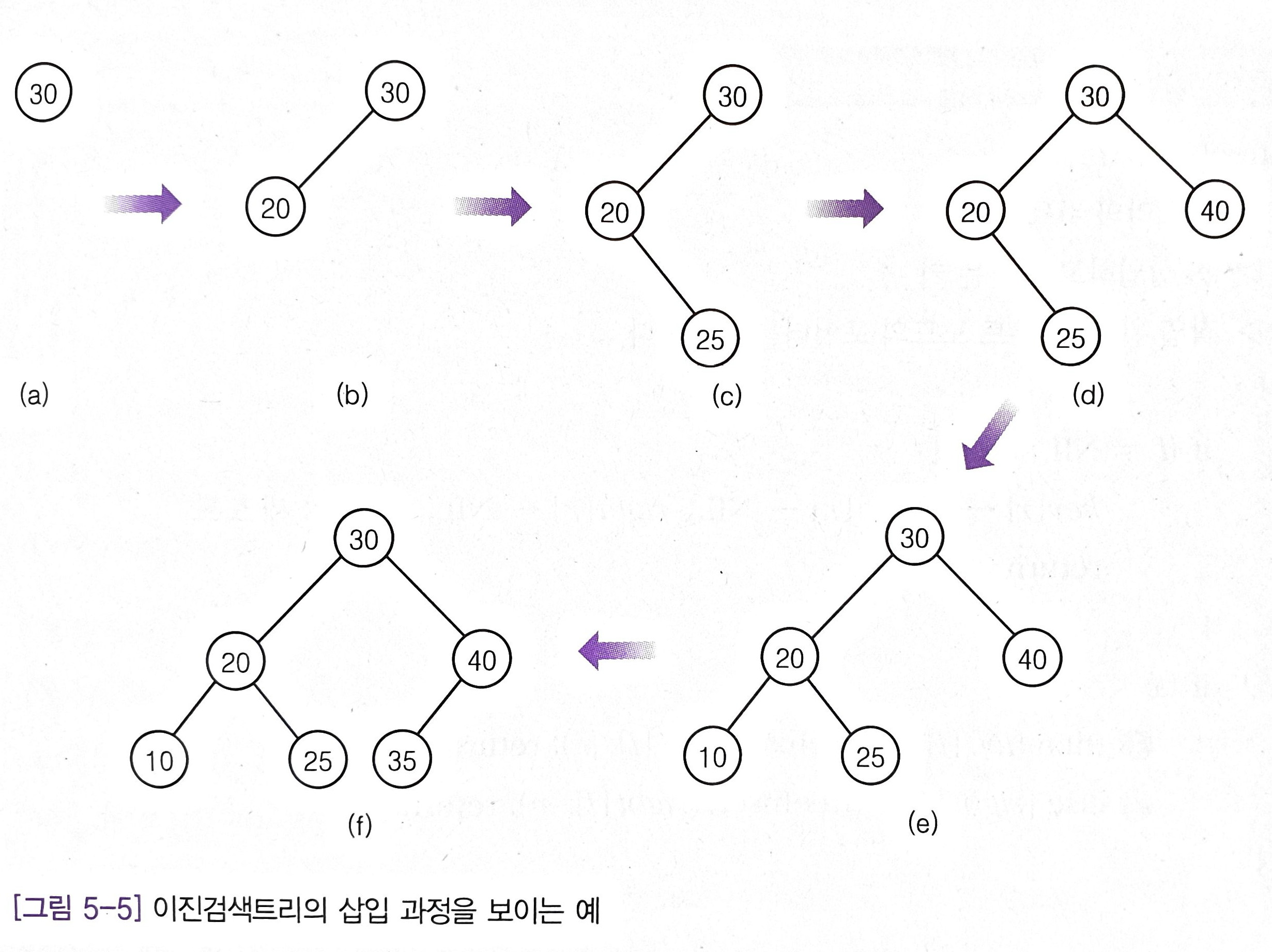
이진 검색 트리에서의 삽입 알고리즘
TreeInsert(t, x)
{
if (t = NIL) then
{
r = NEW_NODE;
key[r] ← x;
left[r] ← NIL;
right[r] ← NIL;
return r;
}
if (x < key[t]) then
{
left[t] ← TreeInsert(left[t], x);
return t;
}
else
{
right[t] ← TreeInsert(right[t], x);
return t;
}
}
이진 검색 트리에서의 삭제
이진 검색 트리서 노드를 삭제할 때에는 다음과 같이 케이스를 나눠서 진행해야 한다.
- 삭제할 노드에 자식이 없는 경우
- 삭제할 노드에 자식이 하나 있는 경우
- 삭제할 노드에 자식이 둘 있는 경우
- 자식이 없는 경우
해당 노드를 바로 삭제한다.

- 자식이 하나 있는 경우
해당 노드를 삭제한 뒤 자식 노드를 삭제한 노드의 위치에 놓아준다.

- 자식이 둘 있는 경우
해당 노도를 삭제한 뒤 이진 검색 트리의 서브 트리의 조건을 깨지 않는 자식 노드를 골라 삭제한 노드의 위치에 놓아준다. 이때, 서브 트리의 조건을 깨지 않는 조건은 다음과 같다.
- 오른쪽 자식의 서브 트리에서 가장 작은 값을 가진 노드
- 왼쪽 자식의 서브 트리에서 가장 큰 값을 가진 노드
※ 선택된 노드에 자식이 존재하는 경우 이상의 알고리즘을 재귀적으로 반복한다.

이진 검색 트리에서의 삭제 알고리즘
TreeDelete(t, r, x)
{
if (r = t) then
{
root ← DeleteNode(t);
}
else if (r = left[p]) then
{
left[p] ← DeleteNode(r);
}
else
{
right[p] ← DeleteNode(r);
}
}
DeleteNode(r)
{
if (left[r] = right[r] = NIL) then
{
return NIL;
}
else if (left[r] = NIL and right[r] ≠ NIL) then
{
return right[r];
}
else if (left[r] ≠ NIL and right[r] = NIL) then
{
return left[r];
}
else
{
s ← right[r];
while (left[s] ≠ NIL)
{
parent ← s;
s ← left[s];
}
key[r] ← key[s];
if (s = right[r]) then
{
right[r] ← right[s];
}
else
{
left[parent] ← right[s];
}
return r;
}
}
이진 검색 트리 구현
연결 자료구조를 이용하여 이진 검색 트리를 구현한다.
BinarySearchTree.h
#pragma once
#include "../Common.h"
#include <string>
#include <queue>
#include <map>
using std::string;
using std::queue;
using std::map;
/// <summary>
/// 이진 검색 트리에 사용할 노드
/// </summary>
struct BinarySearchNode
{
const static int Width = 5;
BinarySearchNode() : isEmpty(false), data{ 0 }, parent{ nullptr },
left{ nullptr }, right{ nullptr } {}
BinarySearchNode(int data) : isEmpty(false), data{ data }, parent{ nullptr },
left{ nullptr }, right{ nullptr } {}
void Clear()
{
data = 0;
parent = nullptr;
left = nullptr;
right = nullptr;
}
int GetMaxDepth()
{
int leftMaxDepth{ left != nullptr ? left->GetMaxDepth() : 0 };
int rightMaxDpth{ right != nullptr ? right->GetMaxDepth() : 0 };
return (leftMaxDepth > rightMaxDpth ? leftMaxDepth : rightMaxDpth) + 1;
}
int GetCurDepth()
{
return (parent != nullptr ? parent->GetCurDepth() : 0) + 1;
}
bool HasLeftChild()
{
return left != nullptr;
}
bool HasRightChild()
{
return right != nullptr;
}
string ToString()
{
if (isEmpty)
{
return string(Width, ' ');
}
string dataStr = std::to_string(data);
size_t spaceCnt = Width - dataStr.size();
size_t leftSpaceCnt = spaceCnt / 2;
size_t rightSpaceCnt = spaceCnt / 2 + spaceCnt % 2;
return string(leftSpaceCnt, '_') + dataStr + string(rightSpaceCnt, '_');
}
bool isEmpty;
int data;
BinarySearchNode* parent;
BinarySearchNode* left;
BinarySearchNode* right;
};
/// <summary>
/// 이진 검색 트리에서 노드의 재활용을 위한 매니저
/// </summary>
class BinarySearchNodeManager
{
public:
~BinarySearchNodeManager();
void Push(BinarySearchNode* node);
BinarySearchNode* Pop();
BinarySearchNode* GetEmptyNode(BinarySearchNode* parent);
private:
BinarySearchNode* nodes;
};
/// <summary>
/// 연결 자료구조를 이용한 이진 검색 트리
/// </summary>
class BinarySearchTree
{
public:
~BinarySearchTree();
bool Exists(int data);
const BinarySearchNode& Search(int data);
void Insert(int data);
void Delete(int data);
void PrintBinarySearchTree();
private:
void Insert(BinarySearchNode* parent, int data);
void Delete(BinarySearchNode* node);
void PrintBinarySearchTree(BinarySearchNode* node, int lineWidth);
BinarySearchNode* GetNode(int data);
bool IsLeftNode(BinarySearchNode* node);
bool IsRightNode(BinarySearchNode* node);
int GetTreeMaxDepth();
string GetNodeStick(BinarySearchNode* node, int blankSize);
private:
BinarySearchNode* _root;
BinarySearchNodeManager _nodeManager;
queue<BinarySearchNode*> _queue;
map<int, string> _numberMap;
map<int, string> _stickMap;
};
BinarySearchTree.cpp
#include "BinarySearchTree.h"
#pragma region 노드 매니저
/// <summary>
/// 종료 전 생성하 노드 제거
/// </summary>
BinarySearchNodeManager::~BinarySearchNodeManager()
{
while (nodes != nullptr)
{
BinarySearchNode* temp{ nodes };
nodes = nodes->left;
delete temp;
}
}
/// <summary>
/// 사용 완료한 노드를 매니저에 저장
/// </summary>
/// <param name="node">사용후 반환할 노드</param>
void BinarySearchNodeManager::Push(BinarySearchNode* node)
{
node->left = nodes;
nodes = node;
}
/// <summary>
/// 노드가 필요한 경우 매니저에서 반환
/// </summary>
/// <returns>사용할 수 있는 노드</returns>
BinarySearchNode* BinarySearchNodeManager::Pop()
{
BinarySearchNode* node{ nodes };
if (node != nullptr)
{
nodes = node->left;
node->Clear();
}
else
{
node = new BinarySearchNode();
}
return node;
}
/// <summary>
/// 주어진 노드를 부모로 하는 공백 노드를 반환한다.
/// </summary>
/// <param name="parent">부모 노드</param>
/// <returns>공백 노드</returns>
BinarySearchNode* BinarySearchNodeManager::GetEmptyNode(BinarySearchNode* parent)
{
BinarySearchNode* emptyNode = Pop();
emptyNode->parent = parent;
emptyNode->isEmpty = true;
return emptyNode;
}
#pragma endregion
#pragma region 이진 검색 트리
/// <summary>
/// 종료 전 남은 노드 제거 처리
/// </summary>
BinarySearchTree::~BinarySearchTree()
{
while (_root != nullptr)
{
Delete(_root);
}
}
/// <summary>
/// 이진 검색 트리에서 특정 값을 가지는 노드가 존재하는지 여부 확인
/// </summary>
/// <param name="data">찾을 값</param>
/// <returns>존재 여부</returns>
bool BinarySearchTree::Exists(int data)
{
BinarySearchNode* node{ _root };
while (node != nullptr)
{
if (node->data == data)
{
return true;
}
else if (node->data > data)
{
node = node->left;
}
else
{
node = node->right;
}
}
return false;
}
/// <summary>
/// 이진 검색 트리에서 주어진 값을 가진 노드를 반환
/// </summary>
/// <param name="data">찾을 값</param>
/// <returns>값을 가진 노드, 없으면 nullptr</returns>
const BinarySearchNode& BinarySearchTree::Search(int data)
{
return *GetNode(data);
}
/// <summary>
/// 이진 검색 트리에 값을 가지는 노드를 삽입
/// </summary>
/// <param name="data">삽입할 값</param>
void BinarySearchTree::Insert(int data)
{
if (Exists(data))
{
return;
}
Insert(_root, data);
}
/// <summary>
/// 이진 검색 트리에서 해당 값을 가지는 노드를 제거
/// </summary>
/// <param name="data">제거할 값</param>
void BinarySearchTree::Delete(int data)
{
if (!Exists(data))
{
return;
}
Delete(GetNode(data));
}
/// <summary>
/// 이진 검색 트리를 출력한다.
/// </summary>
void BinarySearchTree::PrintBinarySearchTree()
{
if (_root == nullptr)
{
std::cout << "EMPTY\n";
return;
}
int maxDepth{ _root->GetMaxDepth() };
int maxNodeCount{ static_cast<int>(std::pow(2, maxDepth - 1)) };
int totalCount{ maxNodeCount * 2 + 1 };
int lineWidth{ totalCount * BinarySearchNode::Width };
for (int i = 1; i <= maxDepth; i++)
{
_numberMap[i] = "";
_stickMap[i] = "";
}
_queue.push(_root);
while (!_queue.empty())
{
BinarySearchNode* node{ _queue.front() };
_queue.pop();
PrintBinarySearchTree(node, lineWidth);
if (!node->isEmpty)
{
if (node->left != nullptr)
{
_queue.push(node->left);
}
else
{
BinarySearchNode* emptyNode{ _nodeManager.GetEmptyNode(node) };
emptyNode->left = node;
_queue.push(emptyNode);
}
if (node->right != nullptr)
{
_queue.push(node->right);
}
else
{
BinarySearchNode* emptyNode{ _nodeManager.GetEmptyNode(node) };
emptyNode->right = node;
_queue.push(emptyNode);
}
}
if (node->isEmpty)
{
_nodeManager.Push(node);
}
}
for (int i = 1; i <= maxDepth; i++)
{
std::cout << _stickMap[i] << '\n';
std::cout << _numberMap[i] << '\n';
}
std::cout << "\n\n";
}
/// <summary>
/// 이진 검색 트리 삽입 처리
/// </summary>
/// <param name="parent">삽입해야 할 노드의 부모</param>
/// <param name="data">삽입할 값</param>
void BinarySearchTree::Insert(BinarySearchNode* parent, int data)
{
if (parent == nullptr)
{
BinarySearchNode* node{ _nodeManager.Pop() };
node->data = data;
_root = node;
}
else if (parent->data > data)
{
if (parent->left == nullptr)
{
BinarySearchNode* node{ _nodeManager.Pop() };
node->data = data;
node->parent = parent;
parent->left = node;
}
else
{
Insert(parent->left, data);
}
}
else
{
if (parent->right == nullptr)
{
BinarySearchNode* node{ _nodeManager.Pop() };
node->data = data;
node->parent = parent;
parent->right = node;
}
else
{
Insert(parent->right, data);
}
}
}
/// <summary>
/// 이진 검색 트리 제거 처리
/// </summary>
/// <param name="node">제거할 노드</param>
void BinarySearchTree::Delete(BinarySearchNode* node)
{
BinarySearchNode* parent{ node->parent };
if (node->left == nullptr && node->right == nullptr)
{
if (IsLeftNode(node))
{
parent->left = nullptr;
}
else if (IsRightNode(node))
{
parent->right = nullptr;
}
else
{
_root = nullptr;
}
_nodeManager.Push(node);
}
else if (node->left != nullptr && node->right == nullptr ||
node->left == nullptr && node->right != nullptr)
{
BinarySearchNode* child{ node->left };
if (child == nullptr)
{
child = node->right;
}
if (IsLeftNode(node))
{
parent->left = child;
}
else if (IsRightNode(node))
{
parent->right = child;
}
else
{
_root = child;
}
child->parent = parent;
_nodeManager.Push(node);
}
else
{
BinarySearchNode* child{ node->left };
while (child->right != nullptr)
{
child = child->right;
}
node->data = child->data;
Delete(child);
}
}
/// <summary>
/// 이진 검색 트리를 출력한다.
/// </summary>
/// <param name="node">현재 출력할 노드</param>
void BinarySearchTree::PrintBinarySearchTree(BinarySearchNode* node, int lineWidth)
{
int curDepth{ node->GetCurDepth() };
int curNodeCount{ static_cast<int>(std::pow(2, curDepth - 1)) };
int totalNodeSize{ curNodeCount * BinarySearchNode::Width };
int blankCount{ curNodeCount + 1 };
int totalBlankSize{ lineWidth - totalNodeSize };
int blankSize{ totalBlankSize / blankCount };
string& numberStr{ _numberMap[curDepth] };
numberStr.append(string(blankSize, ' '));
numberStr.append(node->ToString());
string& stickStr{ _stickMap[curDepth] };
stickStr.append(GetNodeStick(node, blankSize));
}
/// <summary>
/// 주어진 값을 가진 노드의 포인터를 반환한다.
/// </summary>
/// <param name="data">찾으려는 값</param>
/// <returns>노드의 포인터</returns>
BinarySearchNode* BinarySearchTree::GetNode(int data)
{
BinarySearchNode* node{ _root };
while (node != nullptr)
{
if (node->data == data)
{
break;
}
else if (node->data > data)
{
node = node->left;
}
else
{
node = node->right;
}
}
return node;
}
/// <summary>
/// 해당 노드가 부모 노드의 왼쪽 자식인지 여부
/// </summary>
/// <param name="node">확인할 노드</param>
/// <returns>왼쪽 자식인지 여부</returns>
bool BinarySearchTree::IsLeftNode(BinarySearchNode* node)
{
return node->parent != nullptr && node->parent->left == node;
}
/// <summary>
/// 해당 노드가 부모 노드의 오른쪽 자식인지 여부
/// </summary>
/// <param name="node">확인할 노드</param>
/// <returns>오른쪽 자식인지 여부</returns>
bool BinarySearchTree::IsRightNode(BinarySearchNode* node)
{
return node->parent != nullptr && node->parent->right == node;
}
/// <summary>
/// 트리의 최대 깊이를 반환한다.
/// </summary>
/// <returns>트리의 최대 깊이</returns>
int BinarySearchTree::GetTreeMaxDepth()
{
return _root != nullptr ? _root->GetMaxDepth() : 0;
}
/// <summary>
/// 주어진 노드에 맞는 막대를 만들어 반환한다.
/// </summary>
/// <param name="node">처리할 노드</param>
/// <returns>막대 노드 문자열</returns>
string BinarySearchTree::GetNodeStick(BinarySearchNode* node, int blankSize)
{
if (node == _root)
{
return "";
}
int halfNodeWidth{ BinarySearchNode::Width / 2 };
int halfBlankSize{ blankSize / 2 };
string result;
if ((node->isEmpty && node->left != nullptr) || IsLeftNode(node))
{
int leftSpaceCnt{ blankSize + halfNodeWidth
- (BinarySearchNode::Width % 2 == 0 ? 1 : 0) };
result.append(string(leftSpaceCnt, ' '));
result.append(node->isEmpty ? " " : "┌");
int rightHypenCnt{ halfBlankSize + halfNodeWidth - 1 };
for (int i = 0; i < rightHypenCnt; i++)
{
result.append(node->isEmpty ? " " : "─");
}
result.append(node->isEmpty ? " " : "┘");
}
else
{
result.append(node->isEmpty ? " " : "└");
int leftHypenCnt{ halfBlankSize + halfNodeWidth - 1 };
for (int i = 0; i < leftHypenCnt; i++)
{
result.append(node->isEmpty ? " " : "─");
}
result.append(node->isEmpty ? " " : "┐");
result.append(string(halfNodeWidth, ' '));
}
return result;
}
#pragma endregion
main.cpp
#include "Common.h"
#include "검색트리/BinarySearchTree.h"
int main()
{
int n = 9;
int* arr;
// 동작 테스트를 위한 값
arr = new int[n]{ 10, 5, 20, 3, 7, 15, 25, 1, 4 };
BinarySearchTree tree;
for (int i = 0; i < n; i++)
{
tree.Insert(arr[i]);
}
tree.PrintBinarySearchTree();
tree.Delete(5);
tree.PrintBinarySearchTree();
tree.Delete(10);
tree.PrintBinarySearchTree();
tree.Delete(15);
tree.PrintBinarySearchTree();
delete[] arr;
}
실행 결과
_10__
┌─────────────┘└─────────────┐
__5__ _20__
┌───────┘└───────┐ ┌───────┘└───────┐
__3__ __7__ _15__ _25__
┌───┘└───┐
__1__ __4__
_10__
┌─────────────┘└─────────────┐
__4__ _20__
┌───────┘└───────┐ ┌───────┘└───────┐
__3__ __7__ _15__ _25__
┌───┘
__1__
__7__
┌─────────────┘└─────────────┐
__4__ _20__
┌───────┘ ┌───────┘└───────┐
__3__ _15__ _25__
┌───┘
__1__
__7__
┌─────────────┘└─────────────┐
__4__ _20__
┌───────┘ └───────┐
__3__ _25__
┌───┘
__1__
NadanKim/Algorithm: 알고리즘 학습 및 예제 코드 작성을 위한 저장소 (github.com)
NadanKim/Algorithm
알고리즘 학습 및 예제 코드 작성을 위한 저장소. Contribute to NadanKim/Algorithm development by creating an account on GitHub.
github.com